Introduction
We are concerned with uniformly bounded solutions of the equation \[\nabla\cdot U=F,\quad U\in L^{\infty}(\mathbb{T}^2,\mathbb{R}^2), \quad F\in L^2_{\#}(\mathbb{T}^2),\] where \(L^2_{\#}(\mathbb{T}^2)\) is the space of \(L^2\) integrable functions over the 2-dimensional torus \(\mathbb{T}^2\) with zero mean.
The classical Helmholtz solution \(U_{Hel}=\nabla\Delta^{-1}F\) is not always uniformly bounded. And what's more, we are not able to construct a solution linearly which is uniformly bounded [BB03].
Inspired by the idea of hierarchical decompositions in image processing [TNV04], Tadmor [Ta09] introduces a constructive procedure to solve the equation: the solution is given by hierarchical decompositions \(U_{Bdd}=\sum u_j\), where the \(\{u_j\}\)'s can be computed recursively by the following minimizers, \[u_{j+1} = \arg\min_{u} \left\{\|u\|_{L^{\infty}} + \lambda_1 2^j\|F-\nabla\cdot(\sum_{k=1}^j u_k) -\nabla\cdot u\|_{L^2}^2\right\}, \quad j=0,1,\cdots.\] Here \(\lambda_1\) is a sufficiently large parameter to avoid trivial solution \(u_1\equiv 0\).
Analysis on the minimization problem and its dual
We rewrite each minimization step of the hierarchical decompositions in the following form, \[\bar{u}=\arg\min_{u} \left\{\|u\|_{L^{\infty}}+\lambda\|f-\nabla\cdot u\|_{L^{2}}^2\right\}.\] Here, we seek a minimizer \(\bar{u}:\mathbb{T}^2\rightarrow\mathbb{R}^2\) with \(L^{\infty}\) norm defined as \(\|u\|_{L^{\infty}}:=\mathrm{ess } \sup_{x} \sqrt{u_1^2(x)+u_2^2(x)}\), \(f\) is an \(L^2\) function with zero mean, which stands for \(\displaystyle F-\nabla\cdot(\sum_{k=1}^j u_k)\), \(j=0,1,\cdots\), and \(\lambda\) is a sufficiently large parameter, which stands for the dy scale \(\lambda_1 2^j, j=0,1,\cdots\). We also assume Neumann boundary condition for the solution \(u\cdot {\mathbf n}=0\) for future simplicity.
To circumvent the difficulty of \(L^{\infty}\) norm, we find the dual problem of the minimization problem \[\bar{r}=\arg\inf_{r}\sup_{\mu\geq 0}\left[\lambda \left\langle r-2f,r\right\rangle +\mu\left(\|\nabla r\|_{L^1}-\frac{1}{2\lambda}\right)\right],\] where \(\bar{r}\) is the optimal residual which satisfies \(\bar{r}=f-\nabla\cdot\bar{u}\).
Applying minimax theorem and Euler-Lagrange equations, we have a PDE system where \(\bar{r}\) is a solution \[(r-f)-2\lambda\left\langle f-r,r\right\rangle \nabla\cdot\left(\frac{\nabla r}{|\nabla r|}\right)=0.\]
Finally, \(\bar{u}\) can be recovered by \[u=2\lambda\left\langle r-f,r\right\rangle \cdot\frac{\nabla r}{|\nabla r|}.\]
Numerical implementation
We solve the problem \(\nabla\cdot U=F\) using its hierarchical decomposition. In each iteration, we solve the minimization problem. There are 3 stages to finish one iteration.
- Find the non-trivial solution \(r_j\) which satisfies the PDE system with \(\lambda=\lambda_j\) and \(f=f_j\),
- Recover \(u_j\),
- Update \(\lambda_{j+1}=2\lambda_j\), \(f_{j+1}=r_j\).
Initially, \(\lambda_1\) should be greater than \((2\|\nabla f\|_{L^1})^{-1}\), and \(f_1=F\). The iteration terminates when \(\|r_j\|_{L^2}\) is sufficiently small. The final solution \(U_{Bdd}\) is the summation of all \(u_j\)'s.
In stage 1, we solve the PDE system using the following iteration method \[r^{(n+1)}_{i,j}=f_{i,j}+\frac{K(r^{(n)})}{h^2}\left[\frac{r^{(n+1)}_{i+1,j}-r^{(n+1)}_{i,j}}{\sqrt{\epsilon^2+(D_{+x}r^{(n)}_{i,j})^2+(D_{0y}r^{(n)}_{i,j})^2}}-\frac{r^{(n+1)}_{i,j}-r^{(n+1)}_{i-1,j}}{\sqrt{\epsilon^2+(D_{+x}r^{(n)}_{i-1,j})^2+(D_{0y}r^{(n)}_{i-1,j})^2}}\right]\] \[+\frac{K(r^{(n)})}{h^2}\left[\frac{r^{(n+1)}_{i,j+1}-r^{(n+1)}_{i,j}}{\sqrt{\epsilon^2+(D_{0x}r^{(n)}_{i,j})^2+(D_{+y}r^{(n)}_{i,j})^2}}-\frac{r^{(n+1)}_{i,j}-r^{(n+1)}_{i,j-1}}{\sqrt{\epsilon^2+(D_{0x}r^{(n)}_{i,j-1})^2+(D_{+y}r^{(n)}_{i,j-1})^2}}\right].\] with initial \(r^{0}=f/2\), and reflect the bounds. Here \(K(r):=2\lambda\left\langle r-f,r\right\rangle\) and \(\epsilon\) is a small number to avoid singularity.
In stage 2, we recover \(u\) by \[ u^{1,(n+1)}_{i+1/2,j}=-\frac{K^{(n)}}{h}\cdot\frac{r^{(n+1)}_{i+1,j}-r^{(n+1)}_{i,j}}{\sqrt{\epsilon^2+(D_{+x}r^{(n)}_{i,j})^2+(D_{0y}r^{(n)}_{i,j})^2}},\quad u^{2,(n+1)}_{i,j+1/2}=-\frac{K^{(n)}}{h}\cdot\frac{r^{(n+1)}_{i,j+1}-r^{(n+1)}_{i,j}}{\sqrt{\epsilon^2+(D_{0x}r^{(n)}_{i,j})^2+(D_{+y}r^{(n)}_{i,j})^2}}.\]
Numerical Experiments
Let \(F=\Delta v\) on \([-1,1]\times[-1,1]\), where \[v(x,y)=\begin{cases}x\cdot|\log r|^{1/3}\cdot e^{-\frac{1}{1-r^2}}&r<1\\0&r\geq 1\end{cases},\] where \(r=\sqrt{x^2+y^2}\).
Helmholtz solution \(U^1_{Hel}\) is unbounded. But hierarchical solution \(U^1_{Bdd}\) is uniformly bounded.
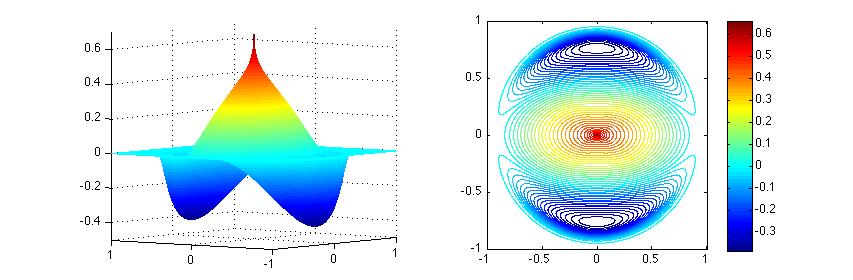
Figure 1. Helmholtz solution \(U^1_{Hel}\)
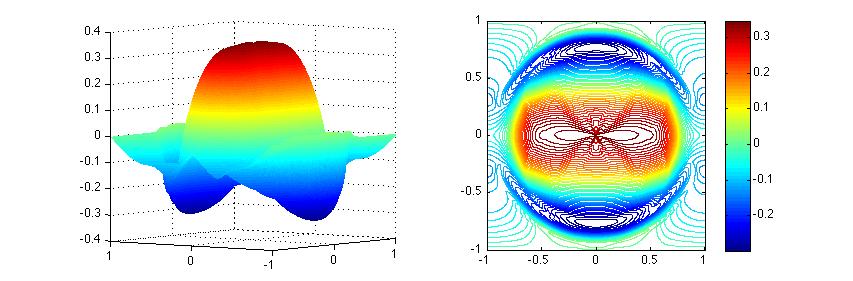
Figure 2. Hierarchical solution \(U^1_{Bdd}\)
We also introduce two steps solution \(U_{2step}=u_1+\nabla\Delta^{-1}r_1\), where \(u_1\) is the result of the first hierarical step, and \(r_1=F-\nabla u_1\). \(U_{2step}\) is also uniformly bounded.
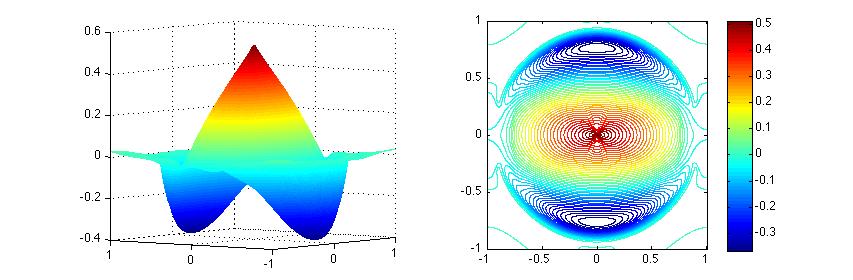
Figure 3. Two steps solution \(U^1_{2step}\)
Resources
- Eitan Tadmor, Changhui Tan. Hierarchical construction of bounded solutions of divU = F in critical regularity spaces. "Nonlinear Partial Differential Equations", Proceedings of the 2010 Abel Symposium held in Oslo, Sep. 2010 (H. Holden & K. Karlsen eds.), Abel Symposia 7, Springer 2011, 255-269. [View PDF]
References
- [AF03] R. Adams and J. Fournier, Sobolev Spaces, 2nd ed., Academic Press, 2003.
- [BB03] J. Bourgain and H. Brezis, On the equation \(\nabla\cdot Y=f\) and application to control of phases, J. Amer. Math. Soc. 16 (2003), no. 2, 393--426.
- [BB07] J. Bourgain and H. Brezis, New estimates for elliptic equations and Hodge type systems, J. Eur. Math. Soc. (JEMS) 9 (2007), no. 2, 277--315.
- [BS88] C. Bennett and R. Sharpley, Interpolation of operators, Pure and Applied Mathematics, vol. 129, Academic Press, Orlando, 1988.
- [Ch04] A. Chambolle, An algorithm for total variation minimization and applications, Journal of Mathematical Imaging and Vision, vol. 20, pp. 89-97, 2004.
- [Co] A. Cohen, private communication.
- [DFT05] B. Dacorogna, N. Fusco and L. Tartar, On the solvability of the equation \(\nabla\cdot u=f\) in \(L^1\) and in \(C^0\), Rend. Mat. Acc. Lincei. s. 9 v. 14 (2003), pp. 239-245.
- [ET99] I. Ekeland and R. Temam, Convex Analysis and Variational Problems, SIAM, 1999.
- [Ev10] L. Evans, Partial Differential Equations, 2nd ed., American Mathematical Society, 2010.
- [Ma06] Y. Maday, \(L^{\infty}\)-stable approximation of a solution to \(\nabla\cdot Y=f\) for \(f\in L^2\) in two dimensions, J. Sci. Comput. 28(2-3) (2006), pp. 451-458.
- [ON63] R. O'Neil, Convolution operators and \(L^{p,q}\) spaces, Duke Math, J. 30, 129-143, 1963.
- [ROF92] L. Rudin, S. Osher and E. Fatemi, Nonlinear Total Variation Based Noise Removal Algorithms, Physica D, 60, pp. 259-268, 1992.
- [Ta89] L. Tartar, Lorentz spaces and applications, Lecture notes, Carnegie Mellon University, 1989.
- [Ta15] E. Tadmor, Hierarchical construction of bounded solutions in critical regularity spaces, Communications on Pure and Applied Mathematics, 2015.
- [TNV04] E. Tadmor, S. Nezzar and L. Vese, A Multiscale Image Representation Using Hierarchical \((BV,L^2)\) Decomposition}, Multiscale Modeling and Simulation: A SIAM Interdisciplinary Journal, Volume 2, Number 4, pp. 554-579, 2004.
- [TNV08] E. Tadmor, S. Nezzar and L. Vese, Hierarchical decomposition of images with applications to deblurring, denoising and segmentation, Communications in Math. Sciences 6(2) (2008) 281-307.









